With the recent and accelerated advances in machine learning (ML), machines can understand natural language, engage in conversations, draw images, create videos and more. Modern ML models are programmed and trained using ML programming frameworks, such as TensorFlow, JAX, PyTorch, among many others. These libraries provide high-level instructions to ML practitioners, such as linear algebra operations (e.g., matrix multiplication, convolution, etc.) and neural network layers (e.g., 2D convolution layers, transformer layers). Importantly, practitioners need not worry about how to make their models run efficiently on hardware because an ML framework will automatically optimize the user’s model through an underlying compiler. The efficiency of the ML workload, thus, depends on how good the compiler is. A compiler typically relies on heuristics to solve complex optimization problems, often resulting in suboptimal performance.
In this blog post, we present exciting advancements in ML for ML. In particular, we show how we use ML to improve efficiency of ML workloads! Prior works, both internal and external, have shown that we can use ML to improve performance of ML programs by selecting better ML compiler decisions. Although there exist a few datasets for program performance prediction, they target small sub-programs, such as basic blocks or kernels. We introduce “TpuGraphs: A Performance Prediction Dataset on Large Tensor Computational Graphs” (presented at NeurIPS 2023), which we recently released to fuel more research in ML for program optimization. We hosted a Kaggle competition on the dataset, which recently completed with 792 participants on 616 teams from 66 countries. Furthermore, in “Learning Large Graph Property Prediction via Graph Segment Training”, we cover a novel method to scale graph neural network (GNN) training to handle large programs represented as graphs. The technique both enables training arbitrarily large graphs on a device with limited memory capacity and improves generalization of the model.
ML compilers
ML compilers are software routines that convert user-written programs (here, mathematical instructions provided by libraries such as TensorFlow) to executables (instructions to execute on the actual hardware). An ML program can be represented as a computation graph, where a node represents a tensor operation (such as matrix multiplication), and an edge represents a tensor flowing from one node to another. ML compilers have to solve many complex optimization problems, including graph-level and kernel-level optimizations. A graph-level optimization requires the context of the entire graph to make optimal decisions and transforms the entire graph accordingly. A kernel-level optimization transforms one kernel (a fused subgraph) at a time, independently of other kernels.
 |
| Important optimizations in ML compilers include graph-level and kernel-level optimizations. |
To provide a concrete example, imagine a matrix (2D tensor):
 |
It can be stored in computer memory as [A B C a b c] or [A a B b C c], known as row- and column-major memory layout, respectively. One important ML compiler optimization is to assign memory layouts to all intermediate tensors in the program. The figure below shows two different layout configurations for the same program. Let’s assume that on the left-hand side, the assigned layouts (in red) are the most efficient option for each individual operator. However, this layout configuration requires the compiler to insert a copy operation to transform the memory layout between the add and convolution operations. On the other hand, the right-hand side configuration might be less efficient for each individual operator, but it doesn’t require the additional memory transformation. The layout assignment optimization has to trade off between local computation efficiency and layout transformation overhead.
If the compiler makes optimal choices, significant speedups can be made. For example, we have seen up to a 32% speedup when choosing an optimal layout configuration over the default compiler’s configuration in the XLA benchmark suite.
TpuGraphs dataset
Given the above, we aim to improve ML model efficiency by improving the ML compiler. Specifically, it can be very effective to equip the compiler with a learned cost model that takes in an input program and compiler configuration and then outputs the predicted runtime of the program.
With this motivation, we release TpuGraphs, a dataset for learning cost models for programs running on Google’s custom Tensor Processing Units (TPUs). The dataset targets two XLA compiler configurations: layout (generalization of row- and column-major ordering, from matrices, to higher dimension tensors) and tiling (configurations of tile sizes). We provide download instructions and starter code on the TpuGraphs GitHub. Each example in the dataset contains a computational graph of an ML workload, a compilation configuration, and the execution time of the graph when compiled with the configuration. The graphs in the dataset are collected from open-source ML programs, featuring popular model architectures, e.g., ResNet, EfficientNet, Mask R-CNN, and Transformer. The dataset provides 25× more graphs than the largest (earlier) graph property prediction dataset (with comparable graph sizes), and graph size is 770× larger on average compared to existing performance prediction datasets on ML programs. With this greatly expanded scale, for the first time we can explore the graph-level prediction task on large graphs, which is subject to challenges such as scalability, training efficiency, and model quality.
 |
| Scale of TpuGraphs compared to other graph property prediction datasets. |
We provide baseline learned cost models with our dataset (architecture shown below). Our baseline models are based on a GNN since the input program is represented as a graph. Node features, shown in blue below, consist of two parts. The first part is an opcode id, the most important information of a node, which indicates the type of tensor operation. Our baseline models, thus, map an opcode id to an opcode embedding via an embedding lookup table. The opcode embedding is then concatenated with the second part, the rest of the node features, as inputs to a GNN. We combine the node embeddings produced by the GNN to create the fixed-size embedding of the graph using a simple graph pooling reduction (i.e., sum and mean). The resulting graph embedding is then linearly transformed into the final scalar output by a feedforward layer.
 |
| Our baseline learned cost model employs a GNN since programs can be naturally represented as graphs. |
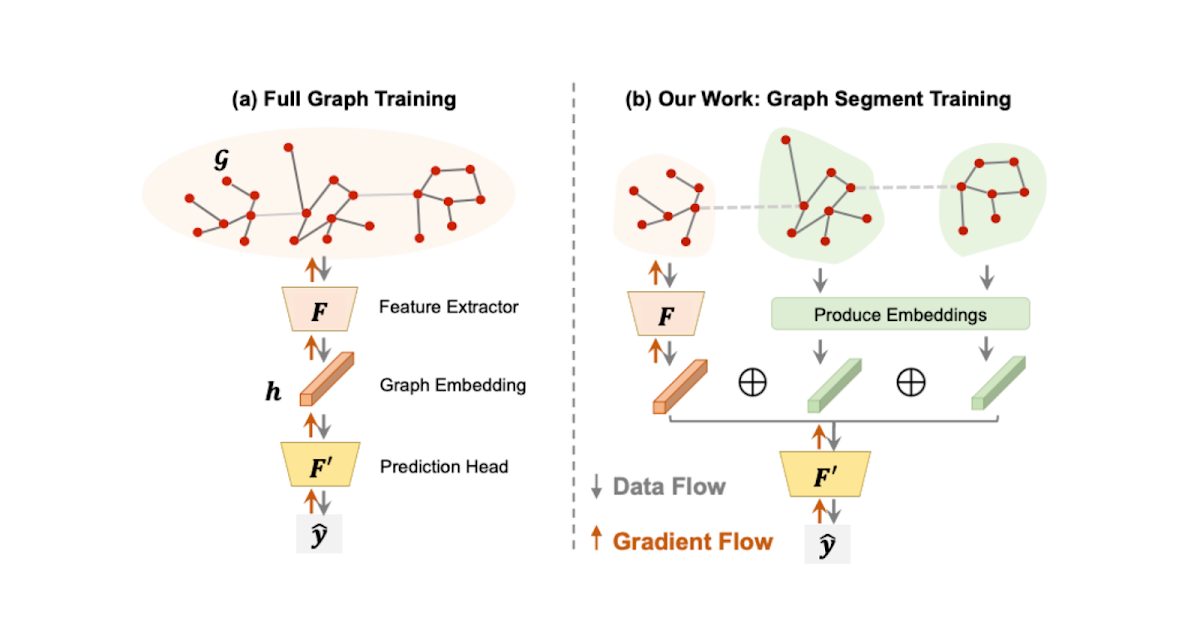
Furthermore we present Graph Segment Training (GST), a method for scaling GNN training to handle large graphs on a device with limited memory capacity in cases where the prediction task is on the entire-graph (i.e., graph-level prediction). Unlike scaling training for node- or edge-level prediction, scaling for graph-level prediction is understudied but crucial to our domain, as computation graphs can contain hundreds of thousands of nodes. In a typical GNN training (“Full Graph Training”, on the left below), a GNN model is trained using an entire graph, meaning all nodes and edges of the graph are used to compute gradients. For large graphs, this might be computationally infeasible. In GST, each large graph is partitioned into smaller segments, and a random subset of segments is selected to update the model; embeddings for the remaining segments are produced without saving their intermediate activations (to avoid consuming memory). The embeddings of all segments are then combined to generate an embedding for the original large graph, which is then used for prediction. In addition, we introduce the historical embedding table to efficiently obtain graph segments’ embeddings and segment dropout to mitigate the staleness from historical embeddings. Together, our complete method speeds up the end-to-end training time by 3×.
 |
| Comparing Full Graph Training (typical method) vs Graph Segment Training (our proposed method). |
Kaggle competition
Finally, we ran the “Fast or Slow? Predict AI Model Runtime” competition over the TpuGraph dataset. This competition ended with 792 participants on 616 teams. We had 10507 submissions from 66 countries. For 153 users (including 47 in the top 100), this was their first competition. We learned many interesting new techniques employed by the participating teams, such as:
- Graph pruning / compression: Instead of using the GST method, many teams experimented with different ways to compress large graphs (e.g., keeping only subgraphs that include the configurable nodes and their immediate neighbors).
- Feature padding value: Some teams observed that the default padding value of 0 is problematic because 0 clashes with a valid feature value, so using a padding value of -1 can improve the model accuracy significantly.
- Node features: Some teams observed that additional node features (such as dot general’s contracting dimensions) are important. A few teams found that different encodings of node features also matter.
- Cross-configuration attention: A winning team designed a simple layer that allows the model to explicitly “compare” configs against each other. This technique is shown to be much better than letting the model infer for each config individually.
We will debrief the competition and preview the winning solutions at the competition session at the ML for Systems workshop at NeurIPS on December 16, 2023. Finally, congratulations to all the winners and thank you for your contributions to advancing research in ML for systems!
NeurIPS expo
If you are interested in more research about structured data and artificial intelligence, we hosted the NeurIPS Expo panel Graph Learning Meets Artificial Intelligence on December 9, which covered advancing learned cost models and more!
Acknowledgements
Sami Abu-el-Haija (Google Research) contributed significantly to this work and write-up. The research in this post describes joint work with many additional collaborators including Mike Burrows, Kaidi Cao, Bahare Fatemi, Jure Leskovec, Charith Mendis, Dustin Zelle, and Yanqi Zhou.