One primary driver for artificial intelligence research in mathematical reasoning is that it may further increase model understanding and problem-solving abilities on complex mathematical problems. Applications such as these can be very important in education, finance, and technology—fields dependent on the accuracy of solutions and the speed at which problems are solved. This improvement in model capabilities can be transferred to enhancing AI’s performance in several special tasks and at logical processes generally.
One of the most important challenges in this area is that large-scale, high-quality datasets designed for mathematical reasoning take time. Traditional methods of building such datasets often require a lot of computational resources and a large amount of seed data, making them hard to scale. This limits the models’ ability to handle a wide variety of math problems, which ends up causing errors—most especially on value variations. This raises the issue of consistency in logic, where models make wrong adjustments to their reasoning due to these variations and hence reduce the reliability of the models.
State-of-the-art techniques to improve mathematical reasoning in AI, such as Chain-of-Thought and Program-of-Thought, either have models reason through a problem step by step or embed computation into their reasoning. Many of these methods, however, have been expensive in terms of dependence on large datasets and computational resources and should be made more scalable. They should also thoroughly model one of the big challenges—inconsistencies that arise naturally when a change in the numerical values of problems leads to wrong deductions.
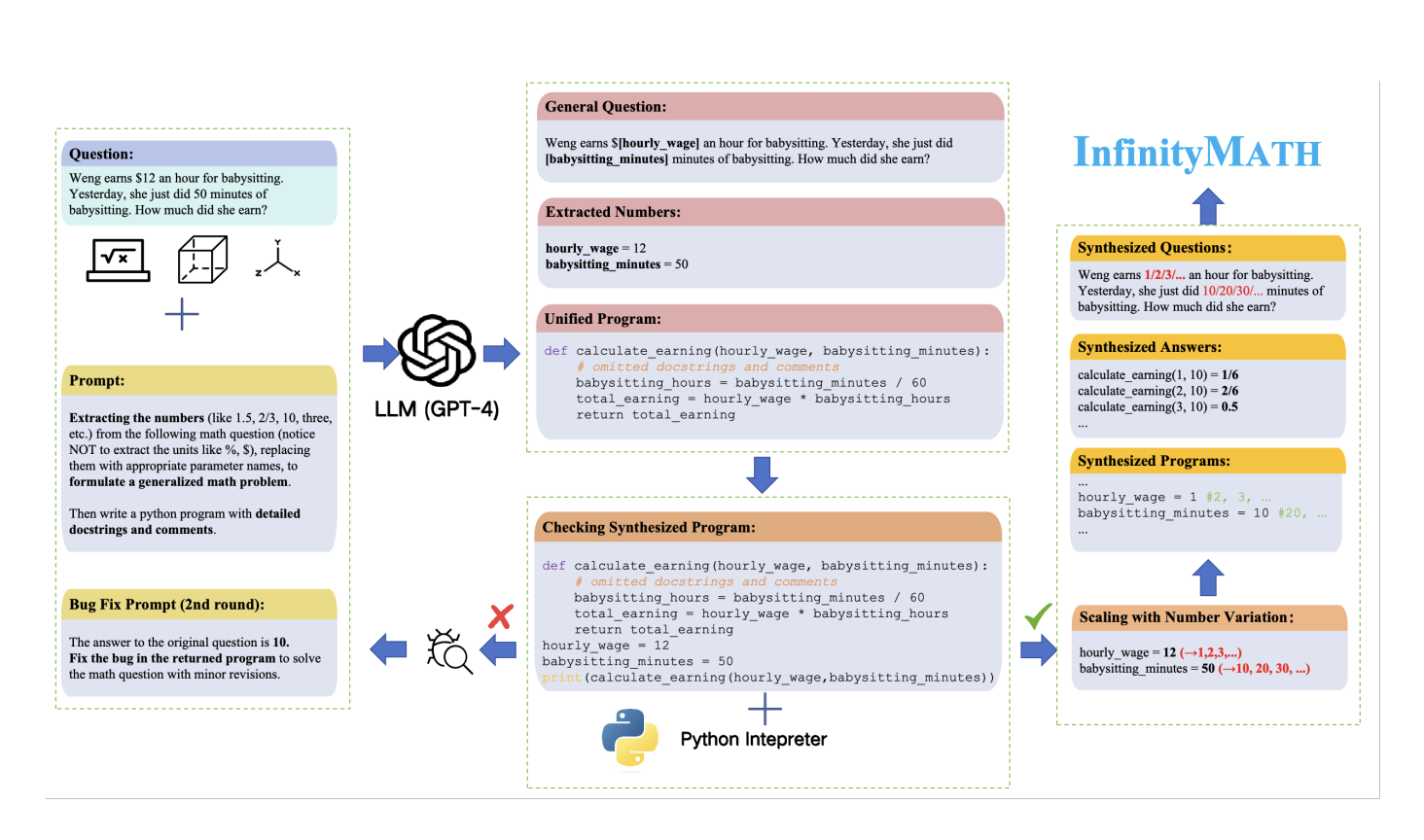
A research team from the Beijing Academy of Artificial Intelligence and China University of Mining & Technology has proposed a scalable dataset for programmatic mathematical reasoning called InfinityMath. According to the authors, InfinityMath is supposed to decouple numeric values from problems stated in mathematics. This way, creating a huge, diverse dataset will require a manageable amount of computational resources. The dataset was created from seven high-quality math sources. It has over 101,380 data points. This makes it quite a comprehensive tool for enhancing the reasoning ability of artificial intelligence models.
The methodology of InfinityMath is multistep for maximum scalability and logical consistency. Masking numerical values of math problems creates generic templates that provide a base for generating problem-solving programs. These are then taken as general templates for developing programs that do not refer to specific numbers, logically following the same reasoning procedure for all possible numerical variations. It can efficiently scale data and improve the resiliency of AI models across different mathematical challenges. Such programs could be generated with sophisticated language models like GPT-4 to reduce potential errors and improve overall quality.
The models fine-tuned with the InfinityMath dataset performed quite well across several benchmarks. For example, aided by the InfinityMath dataset, the Llama2 model showed sensational accuracy improvements in the GSM8K dataset at 316.44% and in the MATH dataset at 1067.6%. Another model fine-tuned on this dataset was CodeLlama, which also showed huge improvements: 120.58% in SVAMP and 1118.09% in SimulEq. These results show that, at the very least, InfinityMath can increase AI models’ accuracy and robustness and improve their reliability in solving various mathematical problems. This consistency was also ahead regarding logical outcomes due to numerical variations; traditional datasets often lack performance.
Therefore, The InfinityMath effect extends beyond mere numerical accuracy to strike at perhaps the most fundamental feature of mathematical reasoning. The authors performed strict, improved evaluations with existing test sets, such as GSM8K+ and MATH+, differing only in the numerical values. Models trained on InfinityMath showed higher performance in logical consistency than any other dataset in accuracy and model efficacy. This success underlines the role played by InfinityMath in further pushing the frontiers of mathematical reasoning and scaling and making an effective solution available to a very large class of AI models.
In other words, InfinityMath is a major improvement in mathematical reasoning, solving two major challenges: scalability and logical consistency. The dataset was curated by a dedicated research team from the Beijing Academy of Artificial Intelligence and the China University of Mining & Technology to ensure that a robust and highly extensible solution could ultimately allow AI models to solve extremely complex mathematical problems. In this case, the InfinityMath process not only separates numerical values from solving processes but also makes constructing a large, highly diversified dataset more efficient to enhance the accuracy and reliability of the AI models. These results thus enable gains in improvement to be witnessed with multiple benchmark-related performances. Therefore, this dataset could further improve AI and its applications in various fields.
Check out the Paper and Dataset. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 48k+ ML SubReddit
Find Upcoming AI Webinars here
Nikhil is an intern consultant at Marktechpost. He is pursuing an integrated dual degree in Materials at the Indian Institute of Technology, Kharagpur. Nikhil is an AI/ML enthusiast who is always researching applications in fields like biomaterials and biomedical science. With a strong background in Material Science, he is exploring new advancements and creating opportunities to contribute.