Large language models (LLMs) face challenges in effectively utilizing additional computation at test time to improve the accuracy of their responses, particularly for complex tasks. Researchers are exploring ways to enable LLMs to think longer on difficult problems, similar to human cognition. This capability could potentially unlock new avenues in agentic and reasoning tasks, enable smaller on-device models to replace datacenter-scale LLMs and provide a path toward general self-improvement algorithms with reduced human supervision. However, current approaches show mixed results, with some studies demonstrating improvements in LLM outputs using test-time computation, while others reveal limited effectiveness on complex tasks like math reasoning. These conflicting findings underscore the need for a systematic analysis of different approaches for scaling test-time computes in LLMs.
Researchers have made significant progress in improving language model performance on mathematical reasoning tasks through various approaches. These include continued pretraining on math-focused data, enhancing the LLM proposal distribution through targeted optimization and iterative answer revision, and enabling LLMs to benefit from additional test-time computation using finetuned verifiers. Several methods have been proposed to augment LLMs with test-time computing, such as hierarchical hypothesis search for inductive reasoning, tool augmentation, and learning thought tokens for more efficient use of additional test-time computing. However, the effectiveness of these methods varies depending on the specific problem and the base LLM used. For easier problems where the base LLM can produce reasonable responses, iterative refinement of initial answers through a sequence of revisions may be more effective. In contrast, for more difficult problems requiring exploration of various high-level approaches, sampling independent responses in parallel or employing tree-search against a process-based reward model might be more beneficial. The analysis of test-time compute scaling in language models, particularly for math reasoning problems where the ground truth is unknown, remains an important area of research.
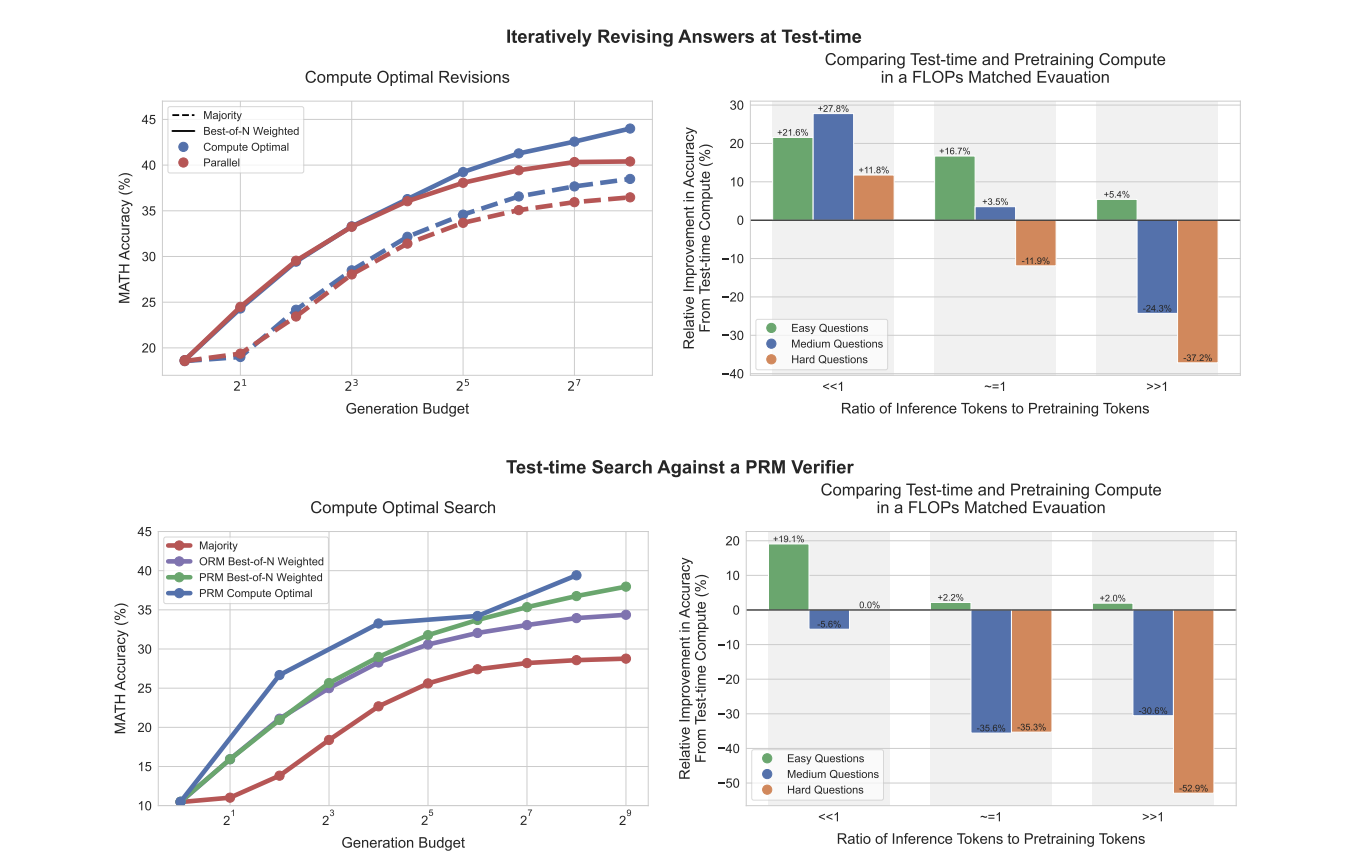
Researchers from UC Berkeley, and Google DeepMind propose an adaptive “compute-optimal” strategy for scaling test-time computing in LLMs. This approach selects the most effective method for utilizing additional computation based on the specific prompt and question difficulty. By utilizing a measure of question difficulty from the base LLM’s perspective, the researchers can predict the efficacy of test-time computation and implement this compute-optimal strategy in practice. This adaptive allocation of test-time compute significantly improves scaling performance, surpassing best-of-N baselines while using approximately 4 times less computation for both revision and search methods. The researchers then compare the effectiveness of their improved test-time compute scaling strategy against the alternative of pretraining larger models.
The use of additional test-time computation in LLMs can be viewed through a unified perspective of modifying the model’s predicted distribution adaptively at test-time. This modification can be achieved through two main approaches: altering the proposal distribution and optimizing the verifier. To improve the proposal distribution, researchers have explored methods such as RL-inspired finetuning (e.g., STaR, ReSTEM) and self-critique techniques. These approaches enable the model to enhance its own outputs at test time by critiquing and revising its initial responses iteratively. Finetuning models on on-policy data with Best-of-N guided improvements have shown promise in complex reasoning tasks.
For verifier optimization, the traditional best-of-N sampling method can be enhanced by training a process-based verifier or process reward model (PRM). This approach allows for predictions of correctness at each intermediate step of a solution, rather than just the final answer. By utilizing these per-step predictions, a more efficient and effective tree search can be performed over the solution space, potentially outperforming naive best-of-N sampling. These methods of modifying the proposal distribution and optimizing the verifier form two independent axes of study in improving test-time computation for language models. The effectiveness of each approach may vary depending on the specific task and model characteristics.
The approach involves selecting optimal hyperparameters for a given test-time strategy to maximize performance benefits. To implement this, the researchers introduce a method for estimating question difficulty, which serves as a key factor in determining the most effective compute allocation. Question difficulty is defined using the base LLM’s performance, binning questions into five difficulty levels based on the model’s pass@1 rate. This model-specific difficulty measure proved more predictive of test-time compute efficacy than hand-labeled difficulty bins. To make the strategy practical without relying on ground-truth answers, the researcher’s approximate question difficulty using a model-predicted notion based on learned verifier scores. This approach allows for difficulty assessment and strategy selection without knowing the correct answer in advance. The compute-optimal strategy is then determined for each difficulty bin using a validation set and applied to the test set. This method enables adaptive allocation of test-time compute resources, potentially leading to significant improvements in performance compared to uniform or ad-hoc allocation strategies.
This study analyzes various approaches for optimizing test-time compute scaling in LLMs, including search algorithms with process verifiers (PRMs) and refining the proposal distribution through revisions. Beam search outperforms best-of-N at lower generation budgets, but this advantage diminishes as budgets increase. Sequential revisions generally outperform parallel sampling, with the optimal ratio between the two depending on question difficulty. Easier questions benefit more from sequential revisions, while harder questions require a balance between sequential and parallel computing. The effectiveness of search methods varies based on question difficulty, with beam search showing improvements on medium-difficulty problems but signs of over-optimization on easier ones. By optimally selecting strategies based on question difficulty and compute budget, the compute-optimal scaling approach can outperform the parallel best-of-N baseline using up to 4x less test-time compute. The study also reveals that test-time computing is more beneficial for easy to medium-difficulty questions or in settings with lower inference loads, while pretraining is more effective for challenging questions or high inference requirements.
This study demonstrates the importance of adaptive “compute-optimal” strategies for scaling test-time computes in LLM’s. By predicting test-time computation effectiveness based on question difficulty, researchers implemented a practical strategy that outperformed best-of-N baselines using 4x less computation. A comparison between additional test-time compute and larger pre-trained models showed that for easy to intermediate questions, test-time compute often outperforms increased pretraining. However, for the most challenging questions, additional pretraining remains more effective. These findings suggest a potential shift towards allocating fewer FLOPs to pretraining and more to inference in the future, highlighting the evolving landscape of LLM optimization and deployment.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 48k+ ML SubReddit
Find Upcoming AI Webinars here
Asjad is an intern consultant at Marktechpost. He is persuing B.Tech in mechanical engineering at the Indian Institute of Technology, Kharagpur. Asjad is a Machine learning and deep learning enthusiast who is always researching the applications of machine learning in healthcare.
