Diffusion models have recently emerged as the de facto standard for generating complex, high-dimensional outputs. You may know them for their ability to produce stunning AI art and hyper-realistic synthetic images, but they have also found success in other applications such as drug design and continuous control. The key idea behind diffusion models is to iteratively transform random noise into a sample, such as an image or protein structure. This is typically motivated as a maximum likelihood estimation problem, where the model is trained to generate samples that match the training data as closely as possible.
However, most use cases of diffusion models are not directly concerned with matching the training data, but instead with a downstream objective. We don’t just want an image that looks like existing images, but one that has a specific type of appearance; we don’t just want a drug molecule that is physically plausible, but one that is as effective as possible. In this post, we show how diffusion models can be trained on these downstream objectives directly using reinforcement learning (RL). To do this, we finetune Stable Diffusion on a variety of objectives, including image compressibility, human-perceived aesthetic quality, and prompt-image alignment. The last of these objectives uses feedback from a large vision-language model to improve the model’s performance on unusual prompts, demonstrating how powerful AI models can be used to improve each other without any humans in the loop.
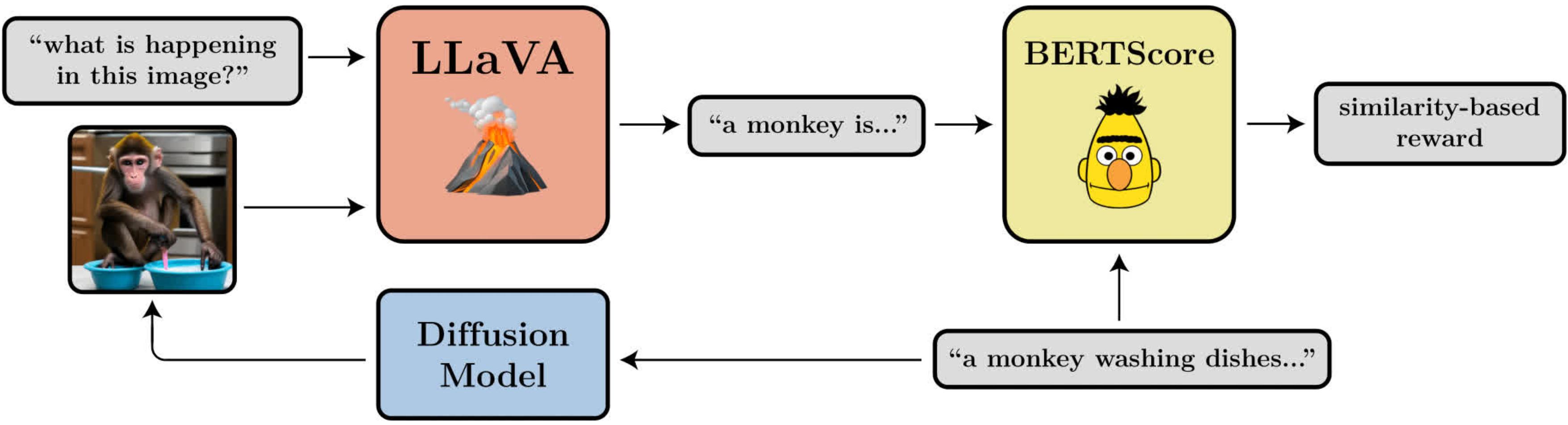
A diagram illustrating the prompt-image alignment objective. It uses LLaVA, a large vision-language model, to evaluate generated images.
Denoising Diffusion Policy Optimization
When turning diffusion into an RL problem, we make only the most basic assumption: given a sample (e.g. an image), we have access to a reward function that we can evaluate to tell us how “good” that sample is. Our goal is for the diffusion model to generate samples that maximize this reward function.
Diffusion models are typically trained using a loss function derived from maximum likelihood estimation (MLE), meaning they are encouraged to generate samples that make the training data look more likely. In the RL setting, we no longer have training data, only samples from the diffusion model and their associated rewards. One way we can still use the same MLE-motivated loss function is by treating the samples as training data and incorporating the rewards by weighting the loss for each sample by its reward. This gives us an algorithm that we call reward-weighted regression (RWR), after existing algorithms from RL literature.
However, there are a few problems with this approach. One is that RWR is not a particularly exact algorithm — it maximizes the reward only approximately (see Nair et. al., Appendix A). The MLE-inspired loss for diffusion is also not exact and is instead derived using a variational bound on the true likelihood of each sample. This means that RWR maximizes the reward through two levels of approximation, which we find significantly hurts its performance.
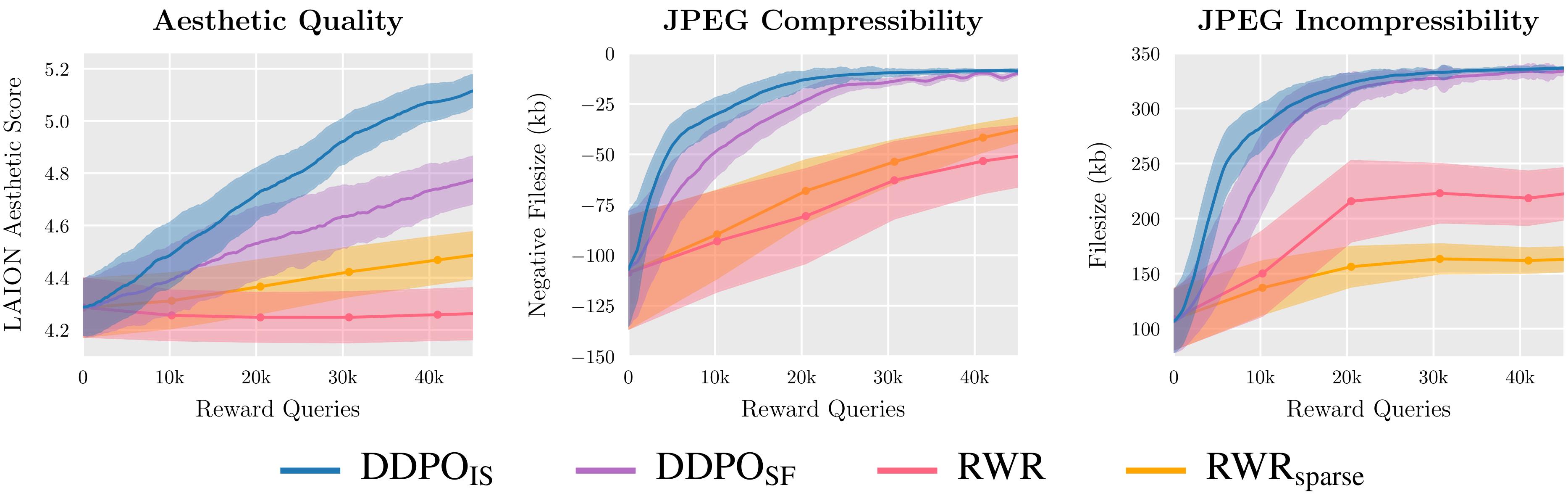
We evaluate two variants of DDPO and two variants of RWR on three reward functions and find that DDPO consistently achieves the best performance.
The key insight of our algorithm, which we call denoising diffusion policy optimization (DDPO), is that we can better maximize the reward of the final sample if we pay attention to the entire sequence of denoising steps that got us there. To do this, we reframe the diffusion process as a multi-step Markov decision process (MDP). In MDP terminology: each denoising step is an action, and the agent only gets a reward on the final step of each denoising trajectory when the final sample is produced. This framework allows us to apply many powerful algorithms from RL literature that are designed specifically for multi-step MDPs. Instead of using the approximate likelihood of the final sample, these algorithms use the exact likelihood of each denoising step, which is extremely easy to compute.
We chose to apply policy gradient algorithms due to their ease of implementation and past success in language model finetuning. This led to two variants of DDPO: DDPOSF, which uses the simple score function estimator of the policy gradient also known as REINFORCE; and DDPOIS, which uses a more powerful importance sampled estimator. DDPOIS is our best-performing algorithm and its implementation closely follows that of proximal policy optimization (PPO).
Finetuning Stable Diffusion Using DDPO
For our main results, we finetune Stable Diffusion v1-4 using DDPOIS. We have four tasks, each defined by a different reward function:
- Compressibility: How easy is the image to compress using the JPEG algorithm? The reward is the negative file size of the image (in kB) when saved as a JPEG.
- Incompressibility: How hard is the image to compress using the JPEG algorithm? The reward is the positive file size of the image (in kB) when saved as a JPEG.
- Aesthetic Quality: How aesthetically appealing is the image to the human eye? The reward is the output of the LAION aesthetic predictor, which is a neural network trained on human preferences.
- Prompt-Image Alignment: How well does the image represent what was asked for in the prompt? This one is a bit more complicated: we feed the image into LLaVA, ask it to describe the image, and then compute the similarity between that description and the original prompt using BERTScore.
Since Stable Diffusion is a text-to-image model, we also need to pick a set of prompts to give it during finetuning. For the first three tasks, we use simple prompts of the form “a(n) [animal]”. For prompt-image alignment, we use prompts of the form “a(n) [animal] [activity]”, where the activities are “washing dishes”, “playing chess”, and “riding a bike”. We found that Stable Diffusion often struggled to produce images that matched the prompt for these unusual scenarios, leaving plenty of room for improvement with RL finetuning.
First, we illustrate the performance of DDPO on the simple rewards (compressibility, incompressibility, and aesthetic quality). All of the images are generated with the same random seed. In the top left quadrant, we illustrate what “vanilla” Stable Diffusion generates for nine different animals; all of the RL-finetuned models show a clear qualitative difference. Interestingly, the aesthetic quality model (top right) tends towards minimalist black-and-white line drawings, revealing the kinds of images that the LAION aesthetic predictor considers “more aesthetic”.

Next, we demonstrate DDPO on the more complex prompt-image alignment task. Here, we show several snapshots from the training process: each series of three images shows samples for the same prompt and random seed over time, with the first sample coming from vanilla Stable Diffusion. Interestingly, the model shifts towards a more cartoon-like style, which was not intentional. We hypothesize that this is because animals doing human-like activities are more likely to appear in a cartoon-like style in the pretraining data, so the model shifts towards this style to more easily align with the prompt by leveraging what it already knows.

Unexpected Generalization
Surprising generalization has been found to arise when finetuning large language models with RL: for example, models finetuned on instruction-following only in English often improve in other languages. We find that the same phenomenon occurs with text-to-image diffusion models. For example, our aesthetic quality model was finetuned using prompts that were selected from a list of 45 common animals. We find that it generalizes not only to unseen animals but also to everyday objects.

Our prompt-image alignment model used the same list of 45 common animals during training, and only three activities. We find that it generalizes not only to unseen animals but also to unseen activities, and even novel combinations of the two.

Overoptimization
It is well-known that finetuning on a reward function, especially a learned one, can lead to reward overoptimization where the model exploits the reward function to achieve a high reward in a non-useful way. Our setting is no exception: in all the tasks, the model eventually destroys any meaningful image content to maximize reward.

We also discovered that LLaVA is susceptible to typographic attacks: when optimizing for alignment with respect to prompts of the form “[n] animals”, DDPO was able to successfully fool LLaVA by instead generating text loosely resembling the correct number.

There is currently no general-purpose method for preventing overoptimization, and we highlight this problem as an important area for future work.
Conclusion
Diffusion models are hard to beat when it comes to producing complex, high-dimensional outputs. However, so far they’ve mostly been successful in applications where the goal is to learn patterns from lots and lots of data (for example, image-caption pairs). What we’ve found is a way to effectively train diffusion models in a way that goes beyond pattern-matching — and without necessarily requiring any training data. The possibilities are limited only by the quality and creativity of your reward function.
The way we used DDPO in this work is inspired by the recent successes of language model finetuning. OpenAI’s GPT models, like Stable Diffusion, are first trained on huge amounts of Internet data; they are then finetuned with RL to produce useful tools like ChatGPT. Typically, their reward function is learned from human preferences, but others have more recently figured out how to produce powerful chatbots using reward functions based on AI feedback instead. Compared to the chatbot regime, our experiments are small-scale and limited in scope. But considering the enormous success of this “pretrain + finetune” paradigm in language modeling, it certainly seems like it’s worth pursuing further in the world of diffusion models. We hope that others can build on our work to improve large diffusion models, not just for text-to-image generation, but for many exciting applications such as video generation, music generation, image editing, protein synthesis, robotics, and more.
Furthermore, the “pretrain + finetune” paradigm is not the only way to use DDPO. As long as you have a good reward function, there’s nothing stopping you from training with RL from the start. While this setting is as-yet unexplored, this is a place where the strengths of DDPO could really shine. Pure RL has long been applied to a wide variety of domains ranging from playing games to robotic manipulation to nuclear fusion to chip design. Adding the powerful expressivity of diffusion models to the mix has the potential to take existing applications of RL to the next level — or even to discover new ones.
This post is based on the following paper:
If you want to learn more about DDPO, you can check out the paper, website, original code, or get the model weights on Hugging Face. If you want to use DDPO in your own project, check out my PyTorch + LoRA implementation where you can finetune Stable Diffusion with less than 10GB of GPU memory!
If DDPO inspires your work, please cite it with:
@misc{black2023ddpo,
title={Training Diffusion Models with Reinforcement Learning},
author={Kevin Black and Michael Janner and Yilun Du and Ilya Kostrikov and Sergey Levine},
year={2023},
eprint={2305.13301},
archivePrefix={arXiv},
primaryClass={cs.LG}
}



